裂区实验设计﹙split-plot design﹚之实务运用

前言：

　　裂区实验设计（split-plot design）是由费雪爵士（Sir Ronald Aylmer Fisher）所发明，起初运用于农业实验，然而许多工业实验在实务上也是以裂区实验设计的方式进行，却被误认为是完全随机实验（completely randomized experiment），因而作了错误的资料分析。

　　当工业实验面临特定实验因子水準不易改变或受限于经济效益之考量（如批量的大小），通常无法进行完全随机实验，也就是实验者必须迁就现实，“刻意”配置实验因子组合的方式，让不易改变的实验因子其改变水準的次数最少化。在这种随机限制（restriction on randomization）的情况下，就必须以裂区实验的架构进行实验，也就要能清楚分辨哪些是属于全区因子（whole-plot factors），哪些是属于副区因子（sub-plot factors），如此才能避免不正确的分析结果。

　　近年来虽然有多位统计专家针对裂区实验发表许多新的应用与解析手法，但在工业实验方面仍然尚未受到应有的重视与了解，本文就先以简单且典型的例子（1），也就是实验配置中包含一个不容易变更水準的实验因子和一个容易变更水準的实验因子，来说明裂区实验的本质以及如何正确的进行裂区实验变异数分析（ANOVA）。

认识裂区实验设计（split-plot design）：

　　以多层陶瓷电容器（Multilayer Ceramic Capacitors）为例，欲探讨烧结炉温度变化（1300°C、1400°C、1500°C）与内部电极不同印刷方法（P1、P2、P3、P4）对电容值的影响程度，因为改变烧结炉温度设定并达到炉内温度均衡相当不容易，因此温度水準变化先採取逐渐升温，再逐渐降温的方式安排，无法採取完全随机的方式进行温度设定，而当每一次炉温达到设定之实验温度时，则将不同印刷方式的陶瓷电容器同时随机放置于烧结炉内不同的位置，实验配置与执行情形，如表一。

　　此类型因为随机限制所导致的实验配置称为裂区设计。因此，裂区实验设计事实上包含两种实验单位（experimental units），也就是全区（whole plot）与副区（sub plot），从表一得知，六次重新设定（reset）不同温度的烧结炉称为全区实验单位，而炉内四个不同的位置则称为副区实验单位。烧结炉温度因为不易变更设定，所以无法与不同的印刷方式做完全随机的实验配置，而有随机上的限制，因此安排为全区因子（whole-plot factors）；而不同的印刷方式则可以轻易的，完全随机的放置于烧结炉内不同的位置，所以安排为副区因子（sub-plot factors）。

　　乍看之下，表一的实验配置情形似乎与“完全随机实验”没有两样，但注意如果按照“完全随机实验”的原则，每一种烧结炉温度必须针对每一种印刷方式重新设定（reset）调温，如此相同的实验规模，则必须进行24次烧结炉的温度重新设定。然而，若是按照裂区实验设计，仅须进行6次烧结炉的温度重新设定，每一次炉温达到设定之实验温度时，再同时将四种印刷方式的陶瓷电容器一起随机放置于炉内不同的位置。但也因为实验配置与进行的方式不同，“裂区实验”与“完全随机实验”的变异数分析方式也就不同。

分析裂区实验设计：

　　从烧结炉加热技术而言，因为烧结炉温度重新设定所产生的实验误差（全区实验误差）将远大于炉内不同位置所产生的实验误差（副区实验误差），所以必须分别推估两种实验单位所对应产生的实验误差，才能正确检定出全区因子、副区因子或是两者之间的交互作用是否有显着的实验效应。

　　因此，必须先将习惯的“完全随机实验”的变异数分析分解成全区与副区两部份，分别探讨其不同的变异来源（sources of variation）并计算其变异。全区部份的变异数分析，如表二，包含温度水準重新设定所产生的变异来源与重覆三种不同温度设定所产生的全区实验误差（whole-plot error）。

　　副区部份的变异数分析，如表三，则包含四种不同印刷方法所产生的变异来源，温度与印刷方法之交互作用所产生的变异来源，和四种不同印刷方法在重覆三种不同温度设定下所产生的副区实验误差（sub-plot error）。 

　　全区部份的变异数分析，因为烧结炉温度重新设定所产生的全区实验误差偏大，自由度也偏低，因此造成统计检定力（power of a statistical test）相对偏低。但本实验之主要目的在比较不同的印刷方法对电容值是否有显着影响，以及印刷方法与温度之间是否存在显着的交互作用，所以副区部份的变异数分析因为副区实验误差相对小，且有相对适当的自由度，已经拥有足够的统计检定力来检出不同的印刷方法和印刷与温度之间交互作用的显着实验效应。

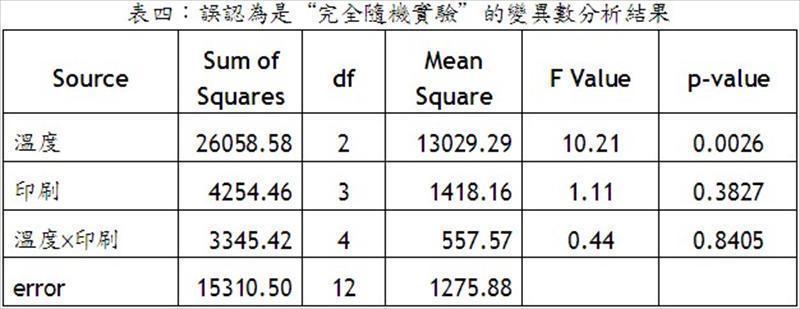
　　本例之裂区实验设计变异数分析中的平方和（Sum of Squares）、自由度（degree of freedom）与均方（Mean Square）的计算方法与一般“完全随机实验”完全相同，但是要特别注意，因为有两个不同的实验误差来源，也就是全区实验误差和副区实验误差，所以必须将变异数分析分解成全区与副区两部份。如果未注意此现象，而採取完全随机实验的方式，进行单一实验误差的变异数分析，将造成不正确的分析结果，如表四。

 

结语

　　在工业实验的领域中，难免会遇到不易变化实验水準的因子，此时裂区实验设计就是可以考虑的另一种选择，因此认知“裂区实验设计”与“完全随机实验”在随机限制上的差异和变异数分析过程的不同，对实验者是有其必要性。

　　从实验成本的角度，每变更一次实验因子的水準必然多产生一笔实验成本，以本例而言，烧结炉温度（全区因子）仅须重新设定温度6次，不必像“完全随机实验”必须进行24次的温度重新设定，因此进行“裂区实验设计”会比相同规模的“完全随机实验”节省许多实验成本。

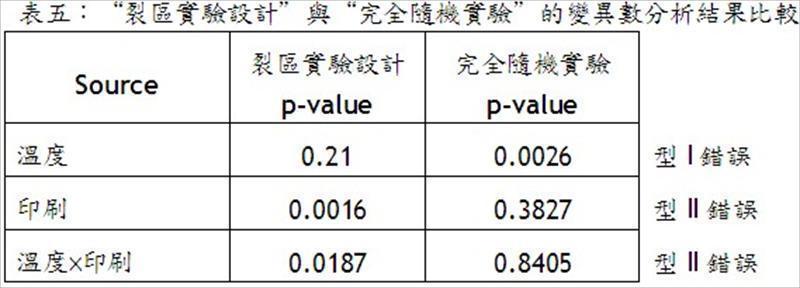
　　但裂区实验设计会产生“全区”和“副区”两种实验误差，若误以完全随机实验的方式进行变异数分析，对全区因子而言，将造成型I错误（type I error）的增加，对副区因子而言，将造成型II错误（type II error）的增加，如表五。所以要切记将变异数分析区分成“全区”和“副区”两大部分，才能同时确保裂区实验设计的实验成本优势与準确的统计检定结果。

 

参考文献

1. Box. G.; Hunter. W.; and Hunter. S.﹙2005﹚. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd edition. New York, NY: Wiley-Inerscience.