前言:
当产品、流程或系统须进行改善时,负责人员常须判断改善前后数据的不同,是由改变的效应所造成,或只是单纯来自实验误差(experimental error)的结果,其实并无显着差异。
以多层陶瓷电容器﹙Multilayer Ceramic Capacitors﹚为例,内部电极厚度﹙inner electrode thickness﹚是网版印刷﹙screen printing﹚製程中相当重要的的品质特性,在“相同”的製程条件设定与生产环境下,不同生产批次所量测的内部电极厚度数据自然就有不同程度的差异。因此当製程工程师须比较供应商所提供的新型网版与现行网版对内部电极厚度是否有不同的效果,进而安排并进行实验后,紧接着就要面临如何分析实验数据,才能合理推断两种网版在印刷製程中对内部电极厚度所造成的效果有显着差异,或是实验观察的结果只是来自实验误差的决策问题。
此时,显着性检定(significance testing),又称为假设检定(hypothesis testing),就在协助我们针对类似上述的效果比较问题,选择适当的检定统计量及运用对应的抽样分配,在可容忍的错误机率前提下,判断实验因子水準(如新型网版与现行网版)改变后的结果,是否存在值得我们注意的显着性差异。
实验误差:
在正式介绍显着性检定的程序之前,先说明实验中产生误差的必然性。
当实验在尽可能相同的条件下重複进行,其实验结果的数据不会完全相同,这种在重複实验情形下所产生的波动称为实验误差。实验误差是由系统的机遇变异原因(chance cause)所造成,是无法避免的,比如:量测仪器和实验设备有限的精度、环境温度与湿度的细微变化、材料本身的纯度问题、以及操作人员的技术等都可能是造成实验误差的因素。
因此实验者必须认知实验误差的存在,对实验误差与相对应的机率理论,﹙根据中央极限定理,实验误差会近似常态分配﹚,要有基本的了解,才能建立将来学习实验设计与分析所必备的扎实基础。但在这里要特别注意实验“误差”不同于实验“错误”,比如:实验条件设定错误、看错或记错量测数据、操作程序或量测程序错误、用错材料等。
统计量﹙statistic﹚与抽样分配﹙sampling distribution﹚:
因为实验误差的存在,实验的反应变数(response variable),如内部电极厚度,是一个随机变数(random variable),其机率结构可用机率分配(probability distribution)来表示。实务上,随机变数机率分配的平均值﹙μ﹚或变异数﹙σ2﹚等母体参数(population parameter)的真值是未知的,必须利用随机样本观测值,透过样本平均值﹙.jpg) ﹚或样本变异数﹙s2﹚的公式,计算得到样本平均值或样本变异数来推估平均值或变异数等母体参数的真值。
﹚或样本变异数﹙s2﹚的公式,计算得到样本平均值或样本变异数来推估平均值或变异数等母体参数的真值。
.jpg)
统计量定义为随机样本观测值的函数,用来推论未知母体参数,因此,.jpg) 和s2均是统计量。而统计量的机率分配称为抽样分配,常态分配、t分配、卡方分配、F分配等都是常见的抽样分配。(只要知道随机样本是来自何种类型的母体分配,通常就能够决定统计量是属于哪一种类型的抽样分配,细节可参阅相关的统计推论书籍﹙1﹚。)
和s2均是统计量。而统计量的机率分配称为抽样分配,常态分配、t分配、卡方分配、F分配等都是常见的抽样分配。(只要知道随机样本是来自何种类型的母体分配,通常就能够决定统计量是属于哪一种类型的抽样分配,细节可参阅相关的统计推论书籍﹙1﹚。)
新型与现行印刷网版的简单比较实验:
在不影响多层陶瓷电容器相关电性与内部电极连续性的前提下,製程工程师希望其内部电极厚度可以愈薄愈好,如此便可以减少内电极膏的单位使用量,进而降低产品单位成本。因此当供应商提供声称可以有效降低内部电极厚度的新型网版时,製程工程师便针对现行网版与新型网版安排并进行完全随机实验﹙completely randomized design﹚,分别蒐集10批内部电极厚度数据,如表1。
.jpg)
表1:新型网版与现行网版内部电极厚度的实验数据﹙um﹚
这种单纯比较两种条件﹙新型网版与现行网版﹚的实验,通常称为简单比较实验。
分别计算两种不同种类网版其内部电极厚度样本平均值︰
新型网版内部电极厚度样本平均值
.jpg)
现行网版内部电极厚度样本平均值
.jpg)
因为在正常的生产过程中,批与批之间的数据本身就有不同程度的差异,即使两种网版内部电极厚度平均值之间有差异,但是否大到足以显示两种网版所造成的效果确实有差异,或是实验观察的差异只是来自实验误差,也许两种网版其实效果相同。显着性检定便是可以帮助工程师回答此问题的一种统计推论方法。
显着性检定(significance testing):
西元1933年,由波兰人奈曼(Jerzy Neyman, 1894-1981),及英国人皮尔生(Egon Pearson, 1895-1980),提出着名的奈曼-皮尔生引理(Neyman - Pearson lemma), 奠定了一套假设检定的架构。
基本上显着性检定可以按照以下的步骤进行
1. 陈述虚无假设与对立假设
2. 选择显着水準
3. 随机抽取样本
4. 计算检定统计量与相对应的p值
5. 决定“拒绝”或“接受” 虚无假设
现在就简要的介绍每一个步骤
陈述虚无假设与对立假设︰
以本文个案为例,虽然供应商宣称在相同的製程条件下,使用新型网版可以降低内部电极厚度,但我们先假设两种网版对内部电极厚度的效果没有差异,再蒐集随机样本,从随机样本中判断是否有“不寻常的证据”足以“拒绝”原先的假设,否则便“接受”原先的假设。
现在把它转换成统计假设问题,首先须陈述虚无假设(null hypothesis),以Ho表示,通常虚无假设表示无差异,而对立假设(alternative hypothesis)则表示有差异,以Ha表示。正式的陈述方式如下:
.jpg)
虽然我们想证明Ha是真的,然而除非证据够强,否则不轻易“拒绝”虚无假设,因为“拒绝”虚无假设时,通常就代表要改变现状,也就是要採用新型网版取代现行网版,当然在作决策前须考虑得更周全。因此要从样本中判断是否有“不寻常的证据”足以“拒绝”原先的假设,只是寻常与不寻常要如何区隔呢?而其中的关键就在于机率。
选择显着水準:
显着水準﹙α﹚就是以机率值来表达,用来量化需要多幺“不寻常的证据”,才能拒绝虚无假设,也就是当随机抽样样本出现的机率值小于α时,便可以拒绝虚无假设,常用的显着水準有0.1,0.05,及0.01等,显着水準愈小,代表需要愈“不寻常的证据”,才能否定虚无假设。
在本案例中,製程工程师指定显着水準α=0.01,表示随机抽样样本出现的机率值小于0.01的事件,可以被视为是机率理论中的小机率事件,也就是长期而言,这样的事件应该在100次试验中平均最多出现一次,因为出现的机率相当低,代表实际上不太可能会发生,而如果在一次的随机抽样中就出现了,便是“不寻常的证据”,因此怀疑原先假设的合理性,进而“拒绝”虚无假设。
随机抽取样本
显着性检定假设实验观测值是独立随机变数﹙independent random variables﹚,只要以随机方式安排实验进行顺序,通常就可以满足此一假设。本文案例的实验顺序便是以随机方式安排进行,如表2。
.jpg)
表2:以随机方式安排实验进行顺序
计算检定统计量与相对应的p值:
如图1所示的盒鬚图﹙box-and-whisker plot﹚,可以让实验者轻易快速的看出两种网版的内部电极厚度数据的变异程度大致上是相同的。(两母体的变异数是否有显着性差异,可以利用F统计量进行检定,细节可参阅相关的统计推论书籍﹙1﹚。)
.jpg)
图1:新型网版与现行网版内部电极厚度的盒鬚图
如果新型网版与现行网版内部电极厚度的变异数无显着性差异,便可以利用to统计量来比较两母体平均数。
.jpg)
其中 和
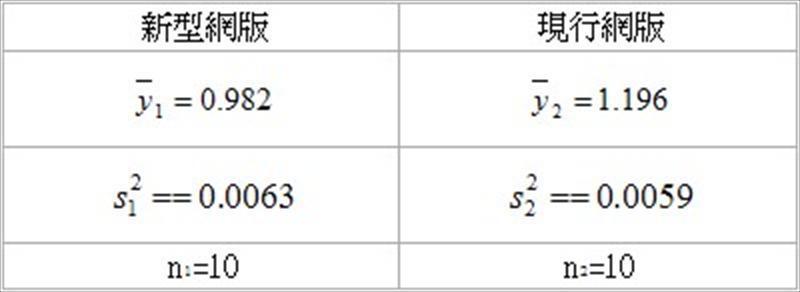
和.jpg) 是样本平均值,n1和n2是样本数, 是共同变异数(common variance)
是样本平均值,n1和n2是样本数, 是共同变异数(common variance)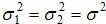 的估计量,其公式为
的估计量,其公式为
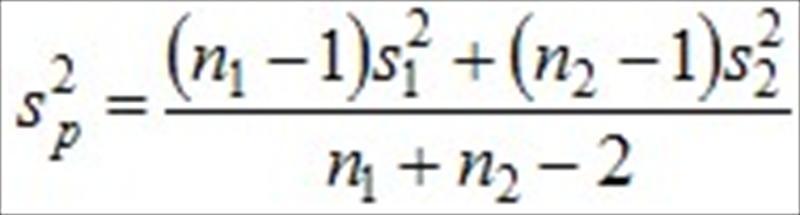
其中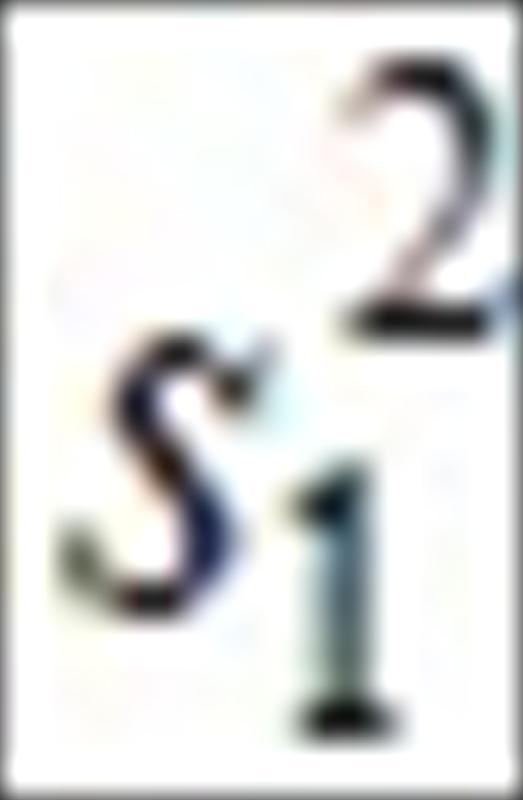 和
和.jpg) 是样本变异数,利用表1的实验数据,可以得到检定统计量
是样本变异数,利用表1的实验数据,可以得到检定统计量
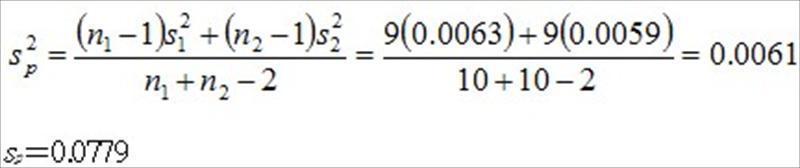
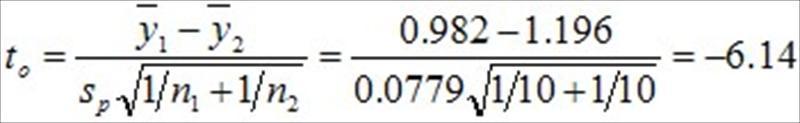
如果Ho为真时,则to检定统计量的抽样分配就是符合自由度为n1+n2-2的t分配,也就是利用t分配,可以描述to检定统计量的机率规律行为。
因为to=-6.14,自由度为18,运用EXCEL软体内建的t分配统计函数,TDIST(x,degrees_freedom,tails),{ 其中x=to=-6.14,degrees_freedom=自由度=18,tails=1表示回传单尾分配,tails=2表示回传双尾分配,本例为双尾检定,因此选择tails = 2 },依序输入函数内所需之数值后,可以轻易计算得到比出现to=-6.14更极端值的累积机率值,也就是p值=0.000008。{ 因为tails = 2,TDIST 以 TDIST = P(|X| > x) = P(X > x or X < -x) 来计算 }。
决定“拒绝”或“接受”虚无假设
在本案例中,指定显着水準α=0.01,因为计算得到p值=0.000008小于α,根据上述小机率事件不应该在一次试验中就出现的原理,也就是说,如果Ho为真时,不应该会出现这样“不寻常”的实验结果,因此怀疑原先假设的合理性,进而“拒绝”虚无假设,所以推论新型网版与现行网版内部电极厚度的平均值有显着性差异。
{ 另一种情形,如果根据实验结果计算得到p值大于α,则代表样本未能提供显着的证据,不能“拒绝”虚无假设,只好“接受”虚无假设 }。
两种错误类型
依据实验数据所推论显着性检定的结果,不论是接受或拒绝虚无假设都有可能会犯错误,以误判的类型而言,事实上有两种可能错误的机率,如表3,一种是当虚无假设为真时,应该接受它,却拒绝它,称为第一类型错误,另一种则是虚无假设不为真时,应该拒绝它,却接受它,称为第二类型错误。
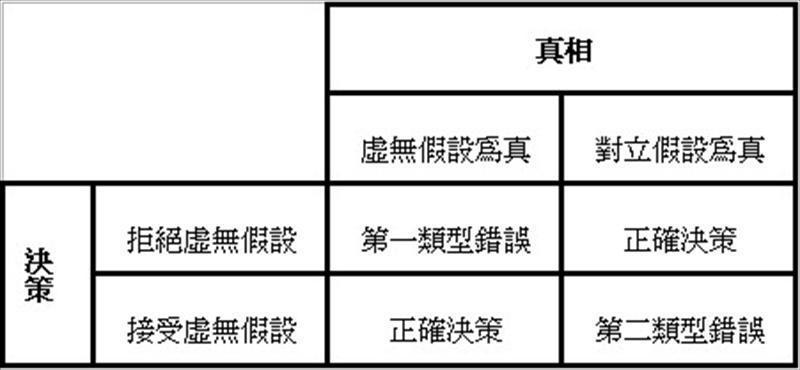
表3:第一类型错误与第二类型错误
第一类型错误,以希腊小写字母α表示,就是前述检定的显着水準,因为在检定的程序中可以事先指定,所以是我们可以直接控制的错误风险。当检定计算所得的p值小于α值时,因为认定如果虚无假设为真时,不应该会出现这样的抽样结果,所以便决定“拒绝”虚无假设,但是当我们做这样的决策时,必须理解虽然发生的机率相当低,仍然“有可能”会发生,因此有可能我们做了错误的决策,这就是所谓的第一类型错误。为儘量避免造成这种错误,因此要採取较保守的α值,也就是0.1,0.05,或0.01,当考量第一类型错误所衍生的负面后果可能愈严重时,就要指定愈小的α值。
第二类型错误,则是以希腊小写字母β表示。而当虚无假设不为真时,可以正确的“拒绝”虚无假设的能力则称为检定力﹙power of test﹚,也就是1减去发生第二类型错误的机率,亦即检定力=1-β,一般建议检定力至少为0.8。在指定显着水準﹙α﹚后,在相同的样本数下,β值会直接受到检定对象的效果差异量﹙effect size﹚的影响,效果差异量愈大,愈容易被发现其存在显着差异,β值就愈低,检定力也就愈高,﹙因为检定力与β两者机率值互补正好为100%﹚,如表4。

表4:双尾t检定,显着水準﹙α﹚=0.01,样本数n1=n2=10,在相同的样本数下,效果差异量愈大,发生第二类型错误的机率愈低,检定力也就愈高。
因此,为确保有足够的检定力可以发现检定对象特定的效果差异量,就要先计算需要抽取的随机样本数大小,方能避免β值过高,如图2。
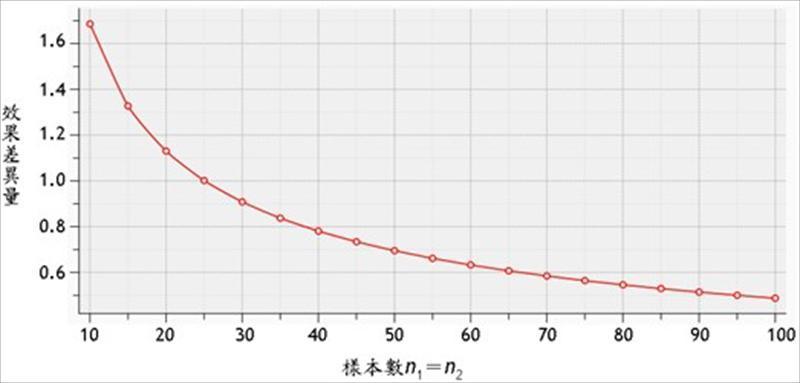
图2︰双尾t检定,显着水準﹙α﹚=0.01 ,为确保检定力至少为0.8,预期侦测的效果差异量﹙﹙μ1-μ2﹚∕σ﹚与样本数之关係。
结语:
在真实的随机世界中所提出的统计假设是否为真,通常都无法百分百确定,只能在现实的条件中,儘可能的减少误判的机率。虽然理想状况是希望两种错误机率皆为0,但通常不存在这种情形,所以进行假设检定时,要事先考虑可以容忍的推论错误机率,以做为判定“拒绝”或“接受”虚无假设的準则。
而显着性检定是以保护虚无假设为原则,因此欲“拒绝”虚无假设,必须掌握“不寻常的证据”,也就是不应该在一次试验中就出现的小机率事件,i.e. p值<显着水準α,发生的机率要够小才能称为显着,除非有显着的差异,否则宁可维持现状。
当“拒绝”虚无假设,认定有显着性差异时,还要分辨统计显着性﹙statistical significance﹚与实务显着性﹙practical significance﹚之间的区别。如果观测的的差异效果,大到某种程度,单纯靠机遇或实验误差产生这种结果的机率很小,也就是差异效果的发生并非偶然时,就称此差异效果有统计显着性。而实务显着性则是指差异效果在真实的世界中是可以产生实际效用。
因为只要样本数足够大,即使是没有实务效益的微小差异也会造成统计显着性。因此当检定结果有统计显着性差异时,还要特别注意其差异在真实的世界中是否有实质意义,也就是要可以反映技术或应用上的具体改善效益等。
参考文献:
1. Montgomery, D. C. ,and Runger, G.C. ﹙2003﹚. Applied statistics and probability for engineers,Wily, New York.



